בעיית תנועה
סעיף א
מהירות המכונית היא 72 קמ”ש, מהירות האופניים 18 קמ”ש.
סעיף ב
המכונית והאופניים יפגשו כעבור 1.4 שעות.
(אלו הם 1 שעות ו- 24 דקות).
- האם אתם צריכים להגדיר משתנה כלשהוא עבור המכונית בדרך כולה?
- הגדירו משתנה ובנו משוואה עבור נקודת הפגישה.
נושא השאלה:
- תשומת לב לכך האם צריך משתנה או לא.
- בעיית פגישה.
- גופים שלא נעים באותו זמן.
1.חישוב מהירות המכונית בדרך כולה
נשים לב שעבור המכונית יש לנו את זמן הנסיעה (מ 8:00 ועד 9:45) וגם את מרחק הנסיעה (126 ק”מ).
לכן ניתן לחשב את המהירות:
72 = 1.75 : 126
מהירות המכונית היא 72 קמ”ש.
2.בניית משוואה עבור נקודת הפגישה
חישוב מהירות האופניים
אנחנו יודעים שסכום הדרכים של המכונית והאופניים בזמן שנפגשו הוא 126 קילומטרים.

הנתונים עבור האופניים
נגדיר
v את מהירות האופניים בקמ”ש.
1 שעה הוא זמן הנסיעה.
1v זה הדרך שהאופניים עברו עד הפגישה.
הנתונים עבור המכונית
מהירות המכונית 72 קמ”ש.
זמן הנסיעה עד הפגישה 1.5 שעות.
108 = 1.5 * 72 זו הדרך שהמכונית עברה.
בניית משוואה
סכום המרחקים הוא 126 ק”מ.
לכן המשוואה היא:
v + 108 = 126 / – 108
v = 18
תשובה: מהירות המכונית היא 72 קמ”ש, מהירות האופניים 18 קמ”ש.
הגדירו את המהירויות החדשות באמצעות a ובנו משוואה אחת עם שני נעלמים.
אחד הנעלמים יתבטל.
a + 72 זו המהירות החדשה של המכונית.
18 – a
המהירות החדשה של האופניים
(t (a + 72 זו הדרך שעברה המכונית ב t זמן.
(t (18 – a זו הדרך שעברו האופניים ב t זמן.
סכום הדרכים ביחד הוא 126 ק”מ.
לכן המשוואה היא:
t (a + 72) + t (18 – a) = 126
at + 72t + 18t -at = 126
90t = 126
t = 1.4
תשובה: המכונית והאופניים יפגשו כעבור 1.4 שעות.
(אלו הם 1 שעות ו- 24 דקות).
גיאומטריה אנליטית
סעיף א
(E (3,2
סעיף ב
(C (9, 0
סעיף ג1
(F (7,0
0.666 = KF
סעיף ג2
שטח המשולש הוא 1.333 יחידות ריבועיות.
נושא השאלה
- גיאמטריה אנליטית ללא מעגל.
- מציאת נקודה על ידי מרחקים שווים.
- מציאת שטח משולש שאחת מצלעותיו מקבילה לצירים.
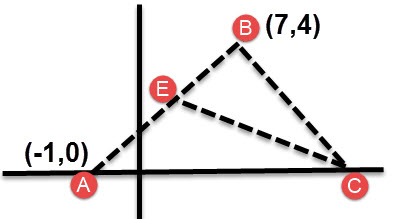
פתרון מקוצר
- מוצאים את הנקודה E על ידי הנוסחה לאמצע קטע.
- ערך ה y בנקודה C הוא 0. רק ערך ה x חסר לנו. נבנה משוואה עם נעלם אחד של EB = EC (הנוסחה למרחק בין שתי נקודות).
- ערך ה x בנקודה K שווה לערך ה x בנקודה K (כי BF מאונך לציר ה x). נמצא את משוואת CE על פי שתי נקודות ונציב את ערך ה x של הנקודה K על מנת למצוא את ערך ה y של הנקודה K.
בנוסף ניתן למצוא את הנקודה F ואז את המרחק KF. - מצאנו את KF, כל שנותן לנו הוא לחשב את הגובה אל KF היוצא מהנקודה E. אורך הגובה הוא הפרש ערכי ה x של הנקודות E ו K.
הנקודה E היא אמצע שתי נקודות הידועות לנו.
סעיף א: מציאת הנקודה E.
E היא אמצע הקטע AB לכן נשתמש בנוסחה לאמצע קטע.
(B(7,4
(A(-1, 0

תשובה: (E (3,2
בעזרת נוסחת מרחק בין שתי נקודות נבנה משוואה:
EB = EC
כאשר הנעלם היחיד במשוואה הזו הוא ערך ה x של הנקודה C.
סעיף ב: מציאת הנקודה C.
הנקודה C נמצאת על ציר ה x. לכן ערך ה y של C הוא 0.
(C (x, 0
נמצא את המרחק EB ואז נציב את המרחק ואת הנקודה C במשוואת מרחק בין שתי נקודות.
1.נמצא את המרחק BE בעזרת הנוסחה למרחק בין שתי נקודות.
(E (3,2) B (7,4
לכן האורך של EB הוא:
EB² = (7 – 3)² + (4 – 2)² =
4² + 2² = 20
2.נציב את הנקודה C בנוסחת המרחק של EC
נגדיר את הנקודה C כ:
(C (x, 0
המרחק של (C (x, 0 מהנקודה (B (7,4 הוא 20√.
לכן על פי נוסחת המרחק בין שתי נקודות:
x – 7)² + (0 – 4)² = 20)
x – 7)² + 16 = 20)
x – 7)² = 4)
נוציא שורש לשני צדדי המשוואה.
בנוסף למשוואה זו שתי פתרונות:
x – 7 = 2
x = 9
או
x – 7 = -2
x = 5
בשאלה אומרים “ערך ה x בנקודה c גדול מערך ה x בנקודה (B (7,4”
לכן התשובה x = 9 היא הנכונה.
(C (9, 0
הנקודה K היא נקודת חיתוך של שני ישרים שאת משוואתם ניתן למצוא.
הנקודה F היא חיתוך עם ציר ה x.
סעיף ג: מציאת הנקודה k ואת אורך הקטע kf.
דרך הפתרון למציאת K:
- נמצא את משוואת CE שנקודה K נמצאת עליה.
- נציב x = 7 במשוואת CE.
פתרון

1.נמצא את משוואת CE.
אנו יודעים:
(C (9, 0
E(3,2)
נשתמש במציאת משוואת ישר על פי שתי נקודות.
![]()
נציב את ערכי הנקודה (C (9, 0 והשיפוע m = -0.333 בנוסחה למציאת משוואת ישר על פי שיפוע ונקודה.
בצורה הזו נמצא את משוואת הישר CE.
(y – y1 = m(x – x1
y – 0 = -0.333 (x – 9
y = -0.333x + 3 (זו משוואת CE).
2.מציאת K.
BF הוא אנך לציר ה x ולכן שומר על ערך x קבוע לכל אורכו.
בנקודה (B (7,4 ערך ה x הוא 7, ולכן גם בנקודה k ערך ה x הוא 7.
נציב במשוואת CE את x = 7.
y = -0.333x + 3
y = -0.333 * 7 + 3 =
-2.333 + 3 = 0.666
הנקודה (K (7, 0.666
3.הנקודה F
נמצאת על ציר ה x, לכן ערך ה y שלה הוא 0.
הישר BF מאונך לציר ה x ולכן שומר על ערך x שווה לכל אורכו.
ערך ה x בנקודה f הוא 7, בדיוק כמו בנקודה B.
(F (7,0
4.המרחק KF.
המרחק בין (K (7, 0.666 ל (F (7,0 הוא על ציר ה y בלבד ושווה ל:
0.666 = 0 – 0.666
את אורך בסיס המשולש KF ניתן לחשב.
הגובה הוא ישר המקביל לציר ה x.
לכן אורך הגובה הוא הפרש שני ערכי x.


את אורך הצלע KF אנו יודעים (0.666).
חישוב אורך הגובה במשולש
- הגובה מאונך לישר המקביל לציר ה y (הישר BF).
- לכן הגובה מקביל לציר ה x ויש לו ערך y קבוע לכל אורכו.
- לכן אורך הגובה הוא הפרש ערכי x של הנקודה E והישר BF.
לכן:
KF = 7 – 3 = 4.
שטח המשולש הוא:
S = (4 * 0.666) : 2 = 1.333
תשובה: שטח המשולש הוא 1.333 יחידות ריבועיות.
הסתברות
סעיף א
מספר האפרסקים שהיה בסל הוא 7.
סעיף ב
ההסתברות שהשני תפוח היא 2/9.
סעיף ג1
ההסתברות להוציא שני פירות מאותו סוג היא 11/18.
סעיף ג2
אם ידוע שיצאו שני פירות מאותו הסוג אז ההסתברות שיצאו שני אפרסקים היא 0.954.
נושא השאלה:
- הגדרת הסתברות בעזרת משתנה.
- הוצאה ללא החזרה.
- חישובים בסיסים בהסתברות + הסתברות מותנה.
נגדיר:
x מספר האפרסקים שבסל.
לכן:
x + 2 מספר הפירות בסל.
ההסתברות שבפעם הראשונה הוציאה תפוח היא:

זו הוצאה ללא החזרה
לכן ההסתברות שבפעם השנייה הוציאה תפוח (לאחר שבפעם הראשונה יצא תפוח):

ההסתברות להוציא תפוח בשני הפעמים היא מכפלת ההסתברויות:

נכפיל במכנה המשותף 36 * (x + 1) (x + 2) ונקבל:
x + 1) (x+ 2) = 2*36)
x² +2x + x + 2 = 72 / -72
x² + 3x -70 = 0
קיבלנו משוואה ריבועית שניתן לפתור בעזרת נוסחת השורשים או פירוק טרינום.
נשתמש בפירוק הטרינום:
x² – 7x + 10x – 70 = 0
x (x – 7) + 10 (x – 7) = 0
x + 10) (x – 7) = 0)
x = -10 או x = 7.
מספר האפרסקים שבסל לא יכול להיות 10-. לכן מספר האפרסקים שהיה בסל הוא 7.
נסכם את המצב בסל לפני ההוצאות:
7 אפרסקים.
2 תפוחים.
9 פירות בסך הכל.
יש שני מצבים בהם הפרי השני הוא תפוח.
- הראשון תפוח והשני תפוח. את ההסתברות הזו חישבנו והיא 1/36.
- הראשון אפרסק והשני תפוח.
נחשב את ההסתברות לאפרסק ראשון והשני תפוח:

נוסיף להסתברות הזו את ההסתברות של תפוח ואז תפוח (1/36).
סך כל ההסתברויות הוא:

תשובה: ההסתברות שהשני תפוח היא 2/9.
יש שתי דרכים להוציא שתי פירות מאותו סוג:
1.שני תפוחים
הסתברות זו חושבה והיא 1/36.
2.שני אפרסקים
נזכור, יש 7 אפרסקים מתוך 9 פירות לפני ההוצאה הראשונה.

סכום ההסתברויות הוא:

תשובה: ההסתברות להוציא שני פירות מאותו סוג היא 11/18.
זו שאלה של הסתברות מותנית.
נגדיר 11/18 = (p (b זו ההסתברות להוציא שני פירות מאותו סוג.
p(a∩b) = 21/36 זו ההסתברות להוציא גם שני אפרסקים וגם שני פירות מאותו הסוג.


תשובה: אם ידוע שיצאו שני פירות מאותו הסוג אז ההסתברות שיצאו שני אפרסקים היא 0.954.
גיאומטריה
סעיף א
הוכחה
סעיף ב
הוכחה
סעיף ג
הוכחה
סעיף ד
SCBD = 1.73R²

על מנת להוכיח ש BA הוא חוצה זווית עלינו להוכיח כי:
∠ABD = ∠CBA
| טענה | נימוק | |
| 1 | ∠ABD = a | הגדרה |
| 2 | ∠AMC = 2a | נתון ∠AMC = 2∠ABD |
| 3 | ∠CBA = 0.5∠ AMC = a | זווית היקפית שווה למחצית הזווית המרכזית הנשענת על אותה קשת |
| 4 | ∠ABD = ∠CBA | נובע מ 1,3 |
שרטוט הפתרון

| טענה | נימוק | |
| 1 | ∠AMC = 2a | מצאנו בסעיף הקודם |
| 2 |
∠CBD = ∠ABD + ∠CBA = 2a |
חיבור זוויות |
| 3 | ∠CBD = ∠AMC = 2a | נובע מ 1,2 |
| 4 | ∠C | זווית משותפת |
| 5 | ΔCBD ∼ ΔCMA | נובע מ 3,4. משולשים דומים על פי משפט דמיון ז.ז. |
שרטוט הפתרון

דרך א:
ידוע כי M הוא אמצע BC(כי BC הוא קוטר ו-M מרכז המעגל)
נשאר להוכיח ש: AM || BD
| טענה | נימוק |
| M אמצע BC | נתון AB קוטר ו-M מרכז המעגל |
| ∠CBD = ∠AMC = 2a | הוכחתי בסעיף ב |
| AM || BD | ישרים בעלי צלעות מתאימות שוות הם מקבילים |
| MA קטע אמצעים | קטע במשולש היוצא מאמצע צלע אחת ומקביל לשנייה הוא קטע אמצעים |
דרך ב
כיוון המחשבה ” M הוא אמצע BC כי הוא מרכז המעגל ו BC הוא קוטר.
נותר להוכיח כי A הוא אמצע DC, כלומר צריך להוכיח ש BA הוא תיכון”
| טענה | נימוק | |
| 1 | M אמצע BC | נתון AB קוטר ו M מרכז המעגל |
| 2 | ∠BAC = 90 | זווית היקפית הנשענת על קוטר גודלה 90. |
| 3 | AB חוצה זוויות וגובה | חוצה זווית הוכחנו ב א. גובה הוכחנו ב 2. |
| 4 | AB תיכון | אם ישר הוא גובה וחוצה זווית במשולש אז המשולש הוא שווה שוקיים והישר הוא גם תיכון. |
| 5 | MA קטע אמצעים | נובע מ 1,4 . ישר במשולש היוצא מאמצע צלע אחת (M) ומגיע לאמצע צלע שנייה (A) הוא קטע אמצעים. |

1.הגדרת BA באמצעות R
מכוון שנתון שמשולש ABM הוא משולש שווה צלעות.
BA = MA = R
2.הגדרת DC באמצעות R
עכשיו צריך להגדיר את DC באמצעות R.
הראנו כי CAB הוא משולש ישר זווית.
על פי משפט פיתגורס במשולש זה:
CA² + AB² = BC²
CA² = BC² – BA²
CA² = (2R)² – R² = 3R²
CA = √3 R
DC = 2CA = 2 * √3 R – מצאנו כי AB תיכון.
3.חישוב שטח המשולש
שטח משולש CBD הוא:
SCBD = 0.5(DC * BA) = 0.5 * 2√3 R * R= √3R² = 1.73R²
טריגונומטריה במישור
סעיף א
SBAD = 75sin α
סעיף ב
α = 60
סעיף ג
BD = 13.23
סעיף ד1
∠ABE = 40.89
סעיף ד2
R = 13.77

על פי הנוסחה הטריגונומטרית לשטח משולש נקבל:
SBAD = 0.5AD * AB * sin α =
0.5 *10 * 15 *sin α = 75sin α
(סעיף זה נפתר בכתיבה מקוצרת ולא מלאה).
צריך לדעת לחשב גם את השטחים של מעוין ומקבילית בעזרת נוסחת השטח הטריגונומטרית.
החישוב אפשרי כי האלכסון יוצר שני משולשים חופפים ושווים בשטחם.
ΔDAB ≅ ΔBCD
על פי צ.צ.צ.
לכן שטח המקבילית שווה לפעמיים מה שמצאנו בסעיף הקודם:
SABCD = 2SBAD = 150sin a = 75√3
sin α = 0.5√3
מכוון שנתון בשאלה ש a < 90 התשובה היחידה שאפשרית היא:
α = 60
במשולש BAD אנו יכולים להשתמש במשפט הקוסינוסים.
BD² = 10² + 15² – 2* 150cos 60
BD² = 325 – 150 = 175
BD = 13.23
את הזווית נוכל למצוא בעזרת משפט הסינוסים במשולש DAB.


בטווח של זוויות במשולש 0-180 הפתרונות הן:
∠ABE = 40.89
או
∠ABE = 139.11
הפתרון השני יוצר בתוך משולש ADB סכום זוויות שהוא גבוה מ 180 ולכן נפסל.
לכן התשובה:
∠ABE = 40.89

על מנת לחשב את רדיוס המעגל החוסם את ABE בעזרת משפט הסינוסים אנו צריכים לדעת צלע וזווית שמולה במשולש.
את AE ניתן לחשב בעזרת משפט הקוסינוסים ואז יהיה לנו צלע וזווית שמולה.
AE² = 26.46² + 15² – 2 * 26.46 * 15 * cos 40.89
AE = 18.03
עכשיו נחשב את רדיוס המעגל החוסם על פי משפט הסינוסים.
![]()
R = 13.77
פונקציית מנה
סעיף א1
x ≠ 3.
סעיף א2
x = 3 היא אסימפטוטה אנכית.
y = 4 היא אסימפטוטה אופקית.
סעיף א3
עליה: x < 3
ירידה: x > 3
סעיף א4

סעיף ב
השטח הכלוא שווה 4.5 יחידות ריבועיות.
סעיף ג
השטח הכלוא שווה 0.5 יחידות ריבועיות.

תחום הגדרה:
עבור x = 3 המכנה מתאפס. חילוק באפס היא פעולה שאינה מוגדרת.
לכן עבור x = 3 הפונקציה אינה מוגדרת.
תחום ההגדרה: x ≠ 3.
אסימפטוטות:
אסימפטוטות אנכיות :
אסימפטוטות אנכיות מתקבלות כאשר הפונקציה שואפת לאינסוף (או מינוס אינסוף).
עבור x = 3 המכנה מתאפס, והמונה הינו מספר שאינו אפס.
כלומר, הפונקציה שואפת לאינסוף.
לכן x = 3 היא אסימפטוטה אנכית.
אסימפטוטות אופקיות:
אסימפטוטות אופקיות יתקבלו כאשר הפונקציה שואפת לערך מסוים,
כאשר x שואף לאינסוף (או מינוס אינסוף).
*כאשר x שואף לאינסוף :
במנה – המונה יהיה מספר קבוע בעוד שהמכנה ישאף לאינסוף, לכן המנה תשאף ל – 0.
המספר 4 אינו תלוי ב- x ולכן הפונקציה כולה תשאף ל – 4.
*כאשר x שואף למינוס אינסוף תתקבל אותה אסימפטוטה.
לכן y = 4 היא אסימפטוטה אופקית.
תחומי עלייה וירידה:
את תחומי העליה והירידה נבדוק בעזרת טבלה.
על מנת לדעת לאילו תחומים עלינו לחלק, נצטרך לבדוק האם יש נקודות קיצון, ואם כן – מה שיעוריהן.
לכן נגזור את הפונקציה ונשווה ל – 0:

נחלק את המונה והמכנה ב- (3-x).
(נוכל לעשות זאת מכיוון שהביטוי x-3 אינו מתאפס בכל תחום הגדרתה של הפונקציה.)

הנגזרת אינה מתאפסת בתחום ההגדרה של הפונקציה. לכן אין נקודות חשודות לקיצון.
נחלק לתחומים לפי נקודת אי ההגדרה של הפונקציה – x = 3.

לכן התשובה:
עליה: x < 3
ירידה: x > 3
סקיצה:


השטח נתון ע”י האינטגרל:

נפתור את האינטגרל:
(נהפוך את השבר לפולינום לפי חוקי חזקות)




תשובה לסעיף ב’ : השטח הכלוא שווה 4.5 יחידות ריבועיות.
g(x) = f(x) - 4
עבור (g(x נוכל לבצע חיסור שטחים, מכיוון שהיא מורכבת מ -2 פונקציות :
1. (f(x שכבר חישבנו - השטח הכלוא שווה 4.5.
2. המספר הקבוע '4'.
כלומר:

מה שנותר לחשב זה האינטגרל הפשוט על המספר הקבוע 4.

![]()
ולכן: (נבצע את החיסור)
g(x) dx = 4.5 - 4 = 0.5∫
תשובה לסעיף ג' : השטח הכלוא שווה 0.5 יחידות ריבועיות.
פונקציית שורש
סעיף א
x ≥ -a
סעיף ב
a = 7
סעיף ג1
ציר x:
(0,0), (7,0-)
ציר y:
(0,0)
סעיף ג2
מקסימום: (7,0-)
מינימום: (216- , 6-)
סעיף ג3

סעיף ג4
חיוביות: x > 0
שליליות: ![]()
סעיף ד
c = 216.
חקרו את הפונקציה:
![]()
תחום הגדרה (כתלות בפרמטר a):
הפונקציה מוגדרת כאשר הביטוי שמתחת לשורש אינו שלילי.
כלומר:
x + a ≥ 0
x ≥ -a
הנקודה (2,24) נמצאת על גרף הפונקציה.
לכן מתקיים: f(2) = 24.
נציב במשוואת הפונקציה:
![]()
![]()
נחלק ב – 8:
3 = (2+a)√
נעלה בריבוע את שני אגפי המשוואה:
a + 2 = 9
a = 7
נקודות חיתוך עם הצירים:
ציר x: נפתור את המשוואה f(x) = 0
x3 * √(x+7) = 0
*x3 = 0
x1 = 0
*x+7) = 0)√
x2 = -7ציר y: נציב x = 0 במשוואת הפונקציה:
f(0) = 0
לכן נקודות החיתוך הן:
ציר x:
(0,0), (7,0-)
ציר y:
(0,0)
נקודות קיצון:
על מנת למצוא נקודות חשודות לקיצון, נגזור את הפונקציה ונשווה ל – 0.
נגזור לפי נגזרת של מכפלה:

מכנה משותף:

המנה שווה ל – 0 רק כאשר המונה מתאפס:
7x3 + 42x2 = 0
נוציא גורם משותף:
x2 * (7x + 42) = 0
x1 = 0, x2 = -6 נקודות חשודות לקיצון.
בנוסף, עבור x = -7 הנגזרת אינה מוגדרת – ולכן היא גם חשודה לקיצון.
נבדוק האם אלו נקודות קיצון לפי תחומי עליה וירידה:

**נשים לב כי x = 0 איננה נקודת קיצון, מכיוון שלפניה ואחריה הפונקציה עולה.
(כלומר הנגזרת אינה משנה את סימנה בנקודה x = 0).
לכן, נקודות הקיצון הן:
מקסימום: (7,0-)
מינימום: (216- , 6-)

תחומי חיוביות ושליליות:
ניתן לראות לפי הסקיצה:
חיוביות: x > 0
שליליות: ![]()
g(x) = f(x) + c , כאשר c הוא פרמטר.
אנו רוצים שגרף הפונקציה (g(x ישיק לציר x.
כלומר, נרצה ששיעור ה -y של נקודת המינימום יהיה 0.
על מנת שזה יקרה, נצטרך להוסיף ל- (f(x קבוע שערכו 216.
(מכיוון ששיעור ה-y הנוכחי של נקודת המינימום הוא 216-).
לכן c = 216.
בעיית קיצון
סעיף א
שיעורי הנקודה A שבעבורה שטח המשולש ABO הוא מקסימלי: (x,y) = (1.5 , 3.375)
סעיף ב
S = 0.84375 = 27/32

נרצה למצוא את נקודה A עבורה שטח המשולש ABO הוא מקסימלי.
נשים לב כי זוהי בעיית קיצון.
לכן, נביע את שטח המשולש ABO כפונקציה של שיעורי הנקודה A.
לאחר מכן נגזור את הפונקציה ונמצא את נקודת המקסימום שלה (שטח מקסימלי של המשולש).
נסמן את שיעור ה-x של נקודה A ב-x.
מכיוון שהנקודה A נמצאת על הפונקציה f(x) = x3 , שיעור ה-y שלה יהיה x3. (הצבת שיעור ה-x בפונקציה).
נקודה B נמצאת באותו שיעור y של נקודה A , ושיעור ה-x שלה הוא 2, מכיוון שנמצאת על הישר x = 2.

כעת נמצא את הפונקציה המבטאת את שטח המשולש ABO.
כלומר, נמצא את שטח המשולש באמצעות שיעורי הנקודות שמצאנו.
נשים לב כי מתקיים:
SΔABO = SABCO – SΔBCO
- שטח הטרפז ABCO:

אורכי הצלעות:
AB = 2 – x
CO = 2
BC = x3
לכן שטח הטרפז הוא:
SABCO = (2 + 2 – x)*x3 / 2
SABCO = (4x3 – x4)/2
SABCO = 2x3 – x4/2
- שטח המשולש BCO:
2/(SΔ = (BC*CO
SΔ = 2*x3/2
SΔBCO = x3
לכן, שטח המשולש ABO:
SΔABO = SABCO – SΔBCO
נציב את השטחים שמצאנו:
SΔABO = 2x3 – x4/2 – x3
SΔABO = x3 – x4/2
נסמן את שטח המשולש כפונקציה, (f(x.
f(x) = x3 – x4/2
כעת נגזור את הפונקציה על מנת למצוא את נקודת המקסימום שלה:
f ‘ (x) = 3x2 – 2x3 = 0
x2 * (3 – 2x) = 0
x1 = 0 – נזכור כי x הוא שיעור ה -x של נקודה A , ולכן זה לא הגיוני שהוא שווה 0. לכן אפשרות זו נפסלת.
x2 = 1.5 – כעת נצטרך לוודא כי אכן מדובר בנקודת מקסימום.

זוהי אכן נקודת מקסימום.
לכן, התשובה:
שיעורי הנקודה A שבעבורה שטח המשולש ABO הוא מקסימלי: (x,y) = (1.5 , 3.375)
על מנת למצוא את שטח המשולש המקסימלי, נציב בפונקציית השטח את שיעור ה – x שמצאנו עבור נקודה A.
S = (1.5)3 – (1.5)4 / 2
S = 3.375 – 5.0625/2
S = 0.84375 = 27/32

האם יש תשובה לשאלה 5?
שלום
דילגו עלייה כנראה בטעות.
נשתדל להשלים בימים הקרובים.
תודה רבה!