נפח קובייה ושטח פנים

לדף זה 5 חלקים:

1. הסבר לנוסחאות קובייה "ותרגילים רגילים"
2. הסבר "לתרגילים הפוכים" בהם נתון הנפח או שטח הפנים.
3. 8 תרגילים עם פתרונות מלאים ופתרונות וידאו. זה החלק החשוב של הדף.
4. קובייה לעומת תיבה – סרטון המסביר את ההבדלים. אם יש לכם קושי עם התרגילים סרטון זה יכול לעזור.
5. פריסה של קובייה – הסבר לפריסה נכונה ולא נכונה של קובייה.

1. נוסחאות נפח ושטח פנים

קובייה היא תיבה מיוחדת שבה אורכי כל המקצועות שווים. כלומר אורך = רוחב = גובה.
נהוג לסמן את אורך מקצוע (צלע) הקובייה באות a.

נפח קובייה
נוסחת נפח קובייה:
V =a³
ניתן לכתוב את הנוסחה גם ללא חזקה:
V = a x a x a

(V הוא הסימון המקובל של נפח. (המילה Volume))

דוגמה לחישוב נפח
אורך מקצוע קובייה הוא 4 סנטימטר.
חשבו את נפח הקובייה.

פתרון
V = 4 * 4 *4 = 64
V = 16 * 4 = 64
תשובה: נפח הקובייה 64 סמ"ק.

שטח פנים של קובייה
S = 6a²
ניתן גם לכתוב את הנוסחה ללא חזקה:
S = 6 * a* a

הסבר לנוסחה
לקובייה 6 פאות שהם ריבועים זהים.
שטח של ריבוע אחד הוא:
S  = a * a = a²

והשטח של 6 ריבועים שהם שטח הפנים הוא:
6a²

דוגמה לחישוב שטח פנים של קובייה
אורך צלע (מקצוע) קובייה הוא 4 סנטימטר.

אם צלע הקובייה היא 4 סנטימטר.
אז שטח של פאה אחת הוא:
16 = 4 *4
ושטח הפנים של הקובייה כולה הוא:
S = 6 * 16 = 96

ניתן גם להציב ישירות בנוסחה:
S = 6 * a* a
S = 6 * 4 *4
S = 24 *4 = 96

תשובה: שטח הפנים של הקובייה הוא 96 סמ"ר.

דוגמה נוספת
חשבו את הנפח ושטח הפנים של תיבה שאורך מקצועה 5.

 

2.שאלות הפוכות

בקובייה אם יודעים את הנפח או את שטח הפנים ניתן למצוא את אורך צלע הקובייה.

3.תרגילים בנושא נפח

מצורפים 9 תרגילים. לתרגילים פתרון כתוב ופתרון בוידאו.
פתרון הוידאו מופיע לאחר הפתרון הכתוב.

תרגילים 1-2 הם תרגילים בסיסיים לחישוב נפח ושטח פנים.
תרגיל 3 דורש ידע בחישוב נפח תיבה ונפח קובייה.
תרגיל 4: כמה פעמים ניתן להכניס קובייה לתיבה?
תרגילים 5-6 הם תרגילים "הפוכים". הנפח או שטח הפנים ידועים ועלינו לחשב את אורך המקצוע.
תרגיל 7 הוא תרגיל הגיון.
בתרגיל 8 יש לכתוב ביטוי אלגברי.

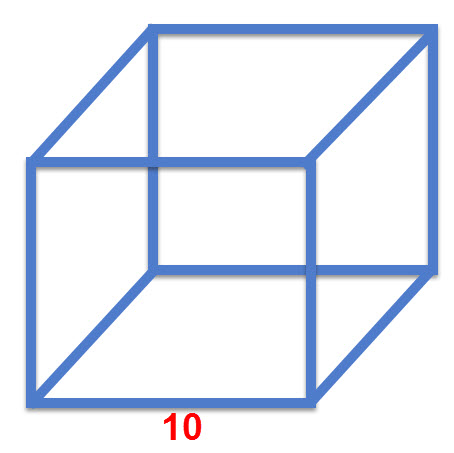
תרגיל 1: חישוב נפח ושטח פנים

נתונה קובייה שאורך הצלע שלה הוא 10 ס"מ.
חשבו את נפחה ושטח הפנים שלה.

תרגיל 2: חישוב נפח ושטח פנים

נתונה קובייה שאורך הצלע שלה היא 1 מטר.
חשבו את הנפח ושטח הפנים של הקובייה.

תרגיל 3: חיסור נפחים

מקובייה שאורך המקצוע שלה הוא 4 סנטימטר "נחתכה" תיבה שאורך המקצועות שלה הם 4,2,1.
חשבו את נפח הגוף החדש שנוצר.