פתרון בגרות 5 יחידות שאלון 581 קיץ 2017

ניתן למצוא את המהירות של נגה בכל אחד מהשלבים על ידי הגדרת המהירות בכל אחד מהשלבים באמצעות x והשוואת השלב הרביעי ל 40.

הטיפ הבא בנושא מציאת הזמן.

זמן הנסיעה הכללי ידוע.
ניתן להגדיר את אורך המסלול כמשתנה.
ומכוון שאנו יודעים את המהירות של כל שלב ניתן גם לבנות משוואה המגדירה את הזמן בכל שלב.

סכום הזמנים הוא 3.75 שעות.

בשאלות מסוג זה כאשר גוף אחד משנה את מהירותו וגוף שני מנסה להשיג אותו יש לחשב את המיקום והזמן של שני הגופים כאשר הגוף שמשנה את מהירותו מסיים לנוע במהירות מסוימת.

במקרה זה יש לחשב את המיקום והזמן של שניהם כאשר נגה מסיימת קטע ואז:

1. לזהות את הקטע שבו נפגשו.
2. לבנות משוואה המוצאת מתי בדיוק נפגשו בקטע זה.

רמז לבניית המשוואה:
שימו לב לנקודת היציאה השונות.

הנושא נלמד במפורט בדף בעיות תנועה 5 יחידות.

סעיף א

אורך המסלול הוא 40 ק”מ.

סעיף ב

דניאל ונגה יפגשו ב 10:30 כאשר הם יהיו במקטע השני.

נמצא את המהירויות של נגה בשלבים השונים

x  המהירות של נוגה בקטע הראשון והאיטי בקמ”ש.
2x המהירות בקטע השני בקמ”ש.
4x המהירות בקטע השלישי בקמ”ש.
8x המהירות בקטע הרביעי בקמ”ש.

המהירות בקטע הרביעי היא 40 קמ”ש ולכן:
8x=40 / :8
x=5

10 קמ”ש בקטע השני,
20, קמ”ש בקטע השלישי.

נגדיר:
y אורכו של המסלול בקמ”ש.
כל מקטע מארבעת הקטעים אורכו 0.25y.
הזמן שלקח לנגה לעשות את המסלול כולו הוא 3.75 שעות.

אנו יודעים את המהירות בכל אחד מהקטעים.
הגדרנו את המרחק של הקטעים.

לכן ניתן נחשב את הזמן שלוקח לעבור את כל אחד מהקטעים:

0.25y : 5 = 0.05y  (קטע ראשון)

0.25y : 10 = 0.025y  (קטע שני)

0.25y : 20 = 0.0125y  (קטע שלישי)

0.25y : 40 = 0.00625y  (קטע רביעי)

נגה רכבה במשך 3 שעות ו 45 דקות. שהם 3.75 שעות.

לכן סכום הזמנים שווה ל 3.75

0.05y + 0.025y + 0.0125y + 0.00625 = 3.75
0.09375y = 3.75
y = 40

תשובה: אורך המסלול הוא 40 ק”מ.

נחשב את המהירות של דניאל:
2 שעות הוא הזמן, 40 קילומטר הוא המרחק.
20= 40:2
20 קמ”ש.

נמצא את המיקום במסלול בו הם נפגשו

נעשה זאת על ידי חישוב המיקום והזמן של שניהם כאשר נוגה מסיימת קטע.

המיקום והזמן כאשר נגה מסיימת את הקטע הראשון
נגה יוצאת ב 8:00 ונוסעת במהירות 5 קמ”ש.
זמן נסיעה בקטע הראשון הוא 2 שעות.
בשעה 10 היא במרחק 10 קילומטר מנקודת ההתחלה.

דניאל יוצא ב 9:45 ובשעה 10:00 עבר
5 = 20 * 0.25
בשעה 10 דניאל נמצא 5 קילומטר מנקודת ההתחלה ולכן הם לא נפגשו.

המיקום והזמן כאשר נוגה מסיימת את הקטע השני.
נגה נסעה 1 שעות במהירות 10 קמ”ש.
לכן בשעה 11:00 היא במרחק 15 קילומטר מנקודת ההתחלה.

דניאל נסע 1 שעה במהירות 20 קמ”ש.
סך הכול עבר עוד 20 קילומטר.
לכן בשעה 11:00 הוא נמצא 25 קילומטר מנקודת ההתחלה.

דניאל עבר מרחק גדול מנגה ולכן הם נפגשו בשלב השני.

מציאת נקודת הפגישה.
כאשר נגה מתחילה את הקטע השני דניאל נמצא 5 קילומטר מאחוריה.
לכן על מנת שיפגשו על דניאל לעבור 5 קילומטר יותר.
(המצב הוא כפי שמתואר בשרטוט של השעה 10).

נניח כי הם נפגשו כעבור t שעות מהזמן שבו נגה מתחילה את הקטע השני.
10t המרחק שנגה תעבור.
20t המרחק שדניאל יעבור.

מכוון שהמרחק בניהם הוא 5 ק”מ המשוואה היא:
10t + 5 = 20t /-10t
10t = 5 /:10
t = 0.5
הזמן הוא 1/2 שעה מאז שנגה התחילה את המקטע השני ו 2.5 שעות מאז שהתחילה את המסלול.

תשובה: דניאל ונגה יפגשו ב 10:30 כאשר הם יהיו במקטע השני.

למטה, שרטוט המתאר שלב הפגישה:

אם נדע שני איברים בסדרה נוכל לדעת בעזרת נוסחת האיבר הכללי כל מה שאנו רוצים על הסדרה.

כאשר נמצא את ערכי c באמצעות המשוואה

c₁ = b₁ – a₁

ועבור איברים נוספים.
ולאחר מיכן נחבר בנפרד את כל איברי C, כל איברי A, כל איברי B נגיע למשוואה המבוקשת.

במהלך הפתרון נגיע  לאי שוויון. נמצא את ה n הראשון עבורו האי שוויון מתקיים ומשם נסיק לאלו ערכי n נוספים האי שווין מתקיים

0.5ⁿ
הוא ביטוי שיורד ככל ש n עולה.

סעיף א
אם יודעים שני איברים בסדרה הנדסית / חשבונית אז ניתן לדעת הכל על הסדרה.

סעיף ב
צריך לדעת לחשב סכום של סדרה בצורה יצירתית.
למשל על ידי כתיבת איברי הסדרה וסכימה שלהם בטור.

סעיף ג
צריך לדעת לפתור אי שוויון כזה.

0.5ⁿ < 0.9

או כזה:

2ⁿ > 20

סעיף א1

b₁ = 2. q=2.

סעיף א2

q=0.5, c₁ = 0.5.

סעיף ב

הוכחה

סעיף ג

n ≥ 4.

על מנת לדעת פרטים על הסדרה b_n עלינו לדעת ערכים של שני איברים שלה.

b₆ = 64

נמצא את b₃ על ידי מציאת a₃.

נמצא את a₃.

b₃ = a₃+c₃ = 7.875 + 0.125  = 8

נמצא את q:

q=2

נמצא את האיבר הראשון
b₃ = b₁q²
8 = 4b₁
b₁ = 2
תשובה: b₁ = 2. q=2.

c₁ = b₁-a₁
נמצא את a₁.

c₁ = 2-1.5=0.5

c₃ / c₁ = q² = 0.125 / 0.5 = 0.25

q² =  0.25
q=0.5
תשובה: q=0.5, c₁ = 0.5.

a_n = b_n – c_n נתון.
c_n = b_n– a_n
קיבלנו כי כל איבר בסדרה c_n שווה להפרש האיברים המתאימים בסדרות b_n, a_n  לכן סכום ההפרשים בסדרות b_n, a_n שווה לסכום הסדרה c_n.

c₁ = b₁ – a₁
……..
c_n = b_n – a_n
כאשר נחבר את הטורים נקבל:

C_n = B_n – A_n

0.9 < B_n – A_n < 1

על פי מה שמצאנו הסעיף הקודם:

0.9 < C_n  < 1

נתון כי c היא סדרה הנדסית.
נציב את הערכים q=0.5, c₁ = 0.5 בנוסחה לסכום סדרה הנדסית ונקבל ביטוי המייצג את סכום סדרה C.

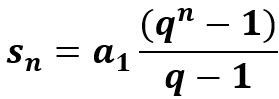
0.9 < C_n  < 1
0.9 < -(0.5ⁿ – 1) < 1

נפתור עכשיו את שני האי שוויונות:
0.5ⁿ-1)<1)-
1-0.5ⁿ <1
0.5ⁿ<0-
אי שוויון זה מתקיים לכל n חיובי ושלם.

0.5ⁿ-1)>0.9)-
1-0.5ⁿ >0.9
0.5ⁿ<0.1

0.5ⁿ זה ביטוי שהולך וקטן ככל ש n עולה.
לכן עלינו למצוא עבור איזה ערך n האי שוויון יתקיים בפעם הראשונה.
וזה גם יתקיים עבור כל n גדול ממנו.

נבדוק טכנית מתי זה קורה:

0.5³ = 0.125 >0.1
0.5⁴ = 1/16 <0.1

n = 4
הוא האיבר הראשון שמקיים את האי שוויון.
האי שוויון מתקיים גם עבור n > 4.

לכן התשובה היא n ≥ 4.

נגדיר: p ההסתברות לבחור אדם עם קלנועית.

עכשיו באמצעות p צריך להגדיר את שתי ההסתברויות ולבנות משוואה.

זו הסתברות מותנה.
צריך לחשב שתי הסתברויות ואז לחלק בניהן.

איך נגרום לכך שבבחירה השישית בדיוק ל 3 תהיה קלנועית?

ב 5 הבחירות הראשונות ל 2 תהיה קלנועית ובבחירה השישית גם קלנועית.

זו שאלת ברנולי “קלאסית”.

בסעיף א: בונים משוואה בעזרת ברנולי.

בסעיף ב: הסתברות מותנית וצריך לחשב ברנולי מספר פעמים.

בסעיף ג: ניסוח מיוחד שצריך להיות מוכנים אליו.

סעיף א

ההסתברות שלנבחר באקראי יש קלנועית היא 0.2.

סעיף ב

0.13844

סעיף ג

0.04096

על מנת לפתור סעיף זה יש להשתמש בנוסחת ברנולי.

P – זו ההסתברות לדגום אדם עם קלנועית.

נחשב את ההסתברות לבחור 4 מ 9.

בעזרת מחשבון מצאנו כי המקדם הבינומי של 4 מ 9 הוא 126.

126P⁴(1-P)⁵  זה הביטוי שנותן את ההסתברות לבחור 4 מ 9.

נחשב את ההסתברות לבחור 6 מ 9.

המקדם הבינומי עבור הסתברות זו הוא 84 (בעזרת מחשבון)

84P⁶(1-P)³  זה הביטוי שנותן את ההסתברות לבחור 6 מ 9.

נבנה משוואה
הביטוי הראשון גדול פי 24 מהראשון לכן המשוואה היא:

84P⁶(1 – P)³ *24 =  126P⁴(1 – P)⁵

2016P² = 126(1 – P)²

16P² = (1 – P)² = 1 – 2P + P²

15P² +2P-1=0

נפתור משוואה זו בעזרת מחשבון:

P = 0.2,

האפשרות השנייה המתקבלת היא שלילית ולכן לא יכולה להיות ערך של הסתברות.

תשובה: ההסתברות שלנבחר באקראי יש קלנועית היא 0.2.

זו שאלה של הסתברות מותנית.
עלינו לחשב:

1. מה ההסתברות של לפחות ל 3 יש קלנועית.
2. ההסתברות שיש קלנועית לבדיוק 4.

ואז לחלק בניהם:

חישוב ההסתברות שלפחות ל 3 יש קלנועית

הסתברות זו מורכבת מ 4 הסתברויות שונות.

ל 3 או 4 או 5 או 6 יש קלנועית.

נחשב כל אחת מהאפשרויות.

ל 3 יש:
המקדם הבינומי של 3 מ 6 הוא 20

T₃ = 20 *0.2³ * 0.8³ = 0.08192

ל 4 יש:
המקדם הבינומי של 4 מ 6 הוא 15

T₄ = 15*0.2⁴*0.8² = 0.01536

ל 5 יש:
T₅ = 6*0.2⁵*0.8 = 0.01536

ל 6 יש:
T₆ = 0.2⁶ = 0.000064

סך כל ההסתברויות במרחב המדגם הוא:

0.110944 = 0.08192+ 0.0136 + 0.01536 + 0.000064

חישוב ההסתברות שבדיוק ל 4 יש קלנועית
חישבנו את ההסתברות הזו למעלה:

T₄ = 0.01536

ההסתברות המבוקשת היא:

תשובה: ההסתברות המבוקשת היא 0.13844

על מנת שזה יקרה צריכים לבחור 2 אנשים על קלנועית מתוך 5 האנשים הראשונים

כמו כן בבחירה השישית האדם השישי צריך להיות עם קלנועית.

נשתמש בנוסחת ברנולי על מנת למצוא את ההסתברות לבחור 2 מ 5.

המקדם הבינומי הוא 10

נציב בנוסחת ברנולי:

10* 0.2² * 0.8³

0.2048 =

נכפיל הסתברות זו בהסתברות לבחור אדם שישי עם קלנועית:

0.04096 = 0.2 * 0.2048

תשובה: ההסתברות היא 0.04096.

1. נגדיר זווית FCE=a∠.
2. DEF=∠FCE = a∠  זווית בין משיק למיתר שווה לזווית ההיקפית הנשענת עליה.
3. OEA = 90∠    רדיוס מאונך למשיק בנקודת ההשקה.
4. OE מקביל ל CD: אם זוויות מתאימות שוות בין ישרים אז הישרים מקבילים.
5. OEC = ∠FCE = a∠  זוויות מתחלפות בין ישרים מקבילים שוות זו לזו
6. OC=0E  רדיוסים שווים זה לזה.
7. OCE = ∠OEC= a∠   במשולש OCE מול צלעות שוות נמצאות זוויות שוות.
8. BCD = ∠OCE + ∠OEC = 2a∠
9. BCD = 2∠DEF∠  נובע מ 2  ו 8.

1. OC=OB: שני רדיוסים.
2. OE קטע אמצעים בטרפז ABCD: אם ישר בטרפז יוצא מאמצע צלע ומקביל לבסיס (הוכחנו ב 4 סעיף קודם) אז הוא קטע אמצעים בטרפז.
3. AE=ED: נובע מ 2.
4. CDA = ∠BAE=90∠ : זוויות חד צדדיות בין ישרים מקבילים בטרפז ישר זווית.
5. BEA = ∠BCE = a∠ : זווית בין משיק למיתר שווה לזווית ההיקפית הנשענת על המיתר.
6. ΔABE≅ΔDFE: משולשים חופפים על פי ז.צ.ז . נובע מ (3,4,5).

1. OE = (AB + DC): 2 = (DF+DC) :2: קטע אמצעים בטרפז שווה לסכום הבסיסים לחלק ב 2.
   וגם AB=DF – צלעות מתאימות בין משולשים חופפים.
2. BC = 2R = 2OE = DF+DC

סעיף א

הוכחה

סעיף ב

a = 17.64

סעיף ג

OE =  1.65r

1. נגדיר OD=X, OE=Y.
2. BO = 2OD=2Y, CO = 2OD=2: תיכונים במשולש מחלקים זה את ביחס של  1:2.
3. COD = ∠BOE∠   זוויות קודקודיות שוות.
4. S_BOE = OE * BO*SIN ∠BOE = Y*2X:2 = 2XY SIN∠BOE
   S_COD = CO*OD* SIN ∠COD = 2XY SIN ∠COD
5. S_BOE = S_COD: נובע מ 3,4.

על מנת לפתור ננסה להגדיר את שטח משולש AOC בעזרת r והזווית המבוקשת בלבד.
r – רדיוס המעגל.
a = ∠ACE

1. tan ACE = r / CD
   CD = r / tan ACE
   AC = 2CD = 2r / tan ACE
2. OD⊥AC: משיק מאונך לרדיוס בנקודת ההשקה.
3. S_AOC = AC * OD:2 = 2r * r / 2tan ACE= r² / tan a
4. שטח המעגל הוא: πr²
5.  πr² = r² / tan a
   tan a = 1/π = 0.318
   a = 17.64

1. sin 17.64 = OD / OC
   OC = OD / SIN 17.64 = r / 0.303 = 3.3r
2. OE = 0.5OC = 1.65r

הגזירה היא ארוכה.

ההזזה g (x) = f(x + 5) אומרת שנרשום x + 5 בכל מקום בו הופיע x בפונקציה f (x).

האם שני האינטגרלים נמצאים במלואם בתחום ההגדרה של הפונקציות?

אם ניקח את השטח בפונקציה אחת עבור אלו ערכים יתקבל בדיוק אותו שטח בפונקציה שנייה?

סעיף א הוא סעיף חקירה יסודי של פונקציית שורש.
צריך לדעת את האלגברה שלו, בדגש על האסימפטוטות והגזירה.

סעיף ב: הוכחה בסיסית של אי זוגיות.
שרטוט הזזה בסיסית של פונקציה.

סעיף ג: הזזה של אינטגרל.

סעיף א1

x > 6 או x < 4

סעיף א2

(1.02- , 0)

סעיף א3

x = 4 , x = 6 , y = -1

סעיף א4

הפונקציה יורדת בתחום x > 6 או x < 4.

סעיף א5

סעיף ב1

הוכחה

סעיף ב2

סעיף ג

הוכחה

על מנת שהפונקציה תהיה מוגדרת הביטוי שבתוך השורש צריך להיות גדול שווה ל 0.
וגם שונה מ 0 (כי השורש הוא המכנה).

x² – 10x + 64 >0
x-6) (x-4) >0)
ניתן לפתור את האי שוויון הריבועי בעזרת שרטוט סקיצה של הפרבולה או בעזרת פתרון של שני אי שוויונים “וגם”.
כאן אשרטט סקיצה:

x > 6 או x < 4 – זה תחום ההגדרה של הפונקציה.

x = 0  נמצא בתחום ההגדרה.
לכן עבור נקודת החיתוך עם ציר ה Y נציב x = 0 ונקבל:

(1.02- , 0)

עבור נקודת החיתוך עם ציר ה x נציב y = 0 ונקבל:

שבר שווה 0 כאשר המונה שווה 0 ולכן:

x – 5 = 0
x = 5

x = 5 הוא מחוץ לתחום ההגדרה לכן אין נקודת חיתוך עם ציר ה x.

אסימפטוטות אופקיות

כאשר x שואף לאינסוף ערכי המונה והמכנה שואפים ל x לכן y=1 הוא אסימפטוטה באינסוף.

ניתן לכתוב זאת כך:
במונה בגלל ש 5- זניח ביחס לאינסוף.
במכנה בגלל שאינסוף בחזקת 1 זניח ביחס לאינסוף בריבוע נקבל:

כאשר x שואף למינוס אינסוף המונה שואף ל x (מינוס אינסוף) ואילו המכנה לערך המוחלט של x לכן y = -1 הוא אסימפטוטה.

ניתן לכתוב זאת כך:

אסימפטוטות אנכיות
נקודות אי ההגדרה של הפונקציה הן x=4,6.
בנקודות הללו המכנה שואף ל 0 ואילו המונה למספר (1 או 1-).
לכן הפונקציה כולה שואפת לאינסוף. לכן x=4 ו x=6 הן אסימפטוטות אנכיות.

נגזור את הפונקציה:

נשים לב שבשבר מימין יש 2 במכנה, נצמצם אותו עם המונה.

המונה שלילי תמיד.
המכנה מורכב משורש החיובי בכל תחום ההגדרה ומביטוי החיובי בכל תחום ההגדרה.

שלילי חלקי חיובי זה שלילי.

לכן הנגזרת שלילית בכל תחום ההגדרה.

הפונקציה יורדת בתחום x > 6 או x < 4.

על מנת לקבל את הפונקציה g (x) = f(x + 5) נרשום x + 5 בכל מקום בו הופיע x בפונקציה f (x).

על מנת להוכיח שהפונקציה אי זוגית נציב x- בפונקציה g(x).

הוכחנו כי (g(x) = – g(-x  ולכן הפונקציה אי זוגית.

g (x) = f(x + 5)

הפונקציה g(x) היא הזזה של 5 יחידות שמאלה מ f(x).
(רמז: כאשר רשום + בתוך ההזזה זזים לכיוון השלילי (ולהפך)).

נשרטט את g(x) על פי f(x).

x > 6 הוא חלק מתחום ההגדרה של f(x).
x > 1 הוא חלק מתחום ההגדרה של g(x).

ומכוון שנתון:

1 < a < b

לכן שני האינטגרלים נמצאים במלואם בתחום ההגדרה של הפונקציות.

סעיף א1

x≠π/2 +πk.

סעיף א2

(0, πk) , (0, 0)

סעיף א3

x = 0.5π + πk

סעיף א4

הפונקציה עולה בכול תחום ההגדרה  x ≠ 0.5π +πk.

סעיף ב

הפונקציה מגדרת כאשר המכנה שונה מ 0.
cos ³ x= 0
cos x = 0

x=π/2 +πk (כאשר k הוא מספר טבעי שלם).
הפונקציה מוגדרת כאשר x≠π/2 +πk.

חיתוך עם ציר ה x
נציב y = 0

שבר שווה 0 כאשר מונה השבר שווה 0.

2sin x =0
sin x =0
x = πk
(0, πk)

חיתוך עם ציר ה y
נציב x = 0

(0, 0)

אסימפטוטה אנכית
כאשר x שואף ל x = 0.5π +πk ערך המונה שואף ל 0 ואילו המונה שואף למספר חיובי.

לכן הפונקציה שואפת לאינסוף / מינוס אינסוף בנקודות הללו והישרים x = 0.5π + πk הם אסימפטוטות אנכיות של הפונקציה.

נגזרת המכנה היא cos⁶x והיא חיובית תמיד ולכן לא משפיעה על סימן הנגזרת.

לכן אגזור מכאן אגזור את המונה בלבד.

בבחינה כאשר אתם גוזרים את המונה בלבד עליכם לרשום ולסמן זאת בצורה בולטת.

f ‘ (x) = 2cos x *cos ³x –  3cos²x (-)sinx * 2sin x  (נגזרת מונה בלבד).
f ‘ (x) =  2cos ⁴x + 6cos²x sin²x
(f ‘ (x) =  2cos ²x(cos²x+ 3sin²x

כאשר cos²x=0 הפונקציה אינה מוגדרת.
הביטוי שבתוך הסוגריים מורכב משני ביטויים בחזקה זוגית שאינם מתאפסים בו זמנית ולכן הביטוי חיובי תמיד.

לכן הנגזרת חיובית בכל תחום ההגדרה והפונקציה עולה בכול תחום ההגדרה  x ≠ 0.5π +πk.

גרף הפונקציה f(x).

סעיף א

t=2, c=8

סעיף ב

x=1+√3
x=1-√3

נתון f (-t)=0 , f(2t) =0.

נציב t- ו 2t במשוואת הפונקציה ונפתור שתי משוואות עם שני נעלמים (t,c).

f (x) = -x² + 2x + c

f (-t) =0 = -(-t)² – 2t + c

t² – 2t + c = 0-

f (2t) =0 = -(2t)² + 2*2t + c

4t²+4t+c=0-

קיבלנו את המשוואות:
4t²+4t+c=0-
t² – 2t + c=0-

נחסר את המשוואות:
3t²+6t=0-
3t (2-t)=0
t=0 או t=2

נתון t>0 ולכן t=2

נציב את הערך של t באחת המשוואות ונקבל את c.
t²-2t+c=0-

c-4-4=0

c=8

תשובה: t = 2, c = 8

ערך ה x בנקודה m הוא ערך ה x של קודקוד הפרבולה.

f (x) = -x² + 2x + 8

x = -2 / -2 = 1

נניח כי הנקודה k היא: (x , -x²+2x+8)

כאשר x>1 שטח המשולש המבוקש הוא:

(S_klm = 0.5(x-1) * (-x²+2x+8

= 0.5 (-x³ + 2x² + 8x + x² – 2x – 8)

= 0.5(-x³ + 3x² + 6x – 8) = -0.5x³ + 1.5x² + 3x – 4

נגזור את הפונקציה s(x) למציאת נקודות קיצון:

s ‘ (x) = -1.5x²  + 3x + 3

נשווה את הנגזרת ל 0:

-1.5x²  + 3x + 3=0

x² – 2x – 2 = 0

נפתור על ידי מחשבון ונקבל:

x=1+√3

x=1-√3

נמצא את הנגזרת השנייה ונציב בה:

s ‘ (x) = -1.5x²  + 3x + 3

s ” (x)= -3x + 3

s ” (x)= 2x – 2

s” (1+√3) < 0 – לכן זו נקודת מקסימום (התשובה המבוקשת).
s” (1-√3) > 0  – לכן זו נקודת מינימום.

נשים לב שבשאלה כתבו “מצאו את שני הפתרונות האפשריים”.

עכשיו מצאנו רק פתרון אחד.

וזה אומר שיש עוד משהו שצריך לחשוב עליו.

בשרטוט של השאלה נתנו לנו את המשולש הזה.

אבל לא אמרו לנו שבהכרח הנקודה L נמצאת מימין ל M.

לכן יכול להתקבל משולש נוסף הנראה כך ובו האורך של ML הוא:

1- x

במקרה זה הפונקציה המתארת את השטח נראית כך:

(S_klm = 0.5(1 – x) * (-x²+2x+8

S_klm = 0.5x³ – 1.5x² – 3x + 4

s ‘ (x) = 1.5x²  – 3x – 3

זו אותה נגזרת כמו הקודמת רק הפוכה בסימן.

לכן במקרה זה היינו מקבלים x=1-√3 נקודת מקסימום.