לדף זה שני חלקים:
- קישורים לדפים מהם אתם יכולים ללמוד את החומר.
- פתרון שאלות מהבגרויות.
1.קישורים
סדרה חשבונית
הדף הרביעי בנושא סכום סדרה חשבונית חשוב יותר מהאחרים וכולל בעצמו עוד מספר קישורים.
- שיעור ראשון: איך מוכיחים שסדרה היא סדרה חשבונית.
- שיעור שני: נוסחת האיבר הכללי.
- שיעור שלישי: כלל הנסיגה.
- שיעור רביעי: סכום סדרה חשבונית (דף הכולל מספר קישורים נוספים).
סדרה הנדסית
- שיעור ראשון: סדרה הנדסית.
- שיעור שני: סכום סדרה הנדסית.
- שיעור שלישי: סכום סדרה הנדסית אינסופית.
2.פתרון בגרויות
התרגילים לקוחים משאלון 581 (לשעבר 806). השאלה בנושא סדרות היא שאלה מספר 2.
המיומנות החשובה ביותר בשאלות בנושא סדרות היא לבנות משוואות ואז להציב משתנה ממשוואה אחת למשוואה שנייה.
קיץ 2019 מועד א
זו שאלה שבה כל פעם נצטרך להציב משוואה אחת במשוואה אחרת על מנת להגיע לביטוי הרצוי.
דבר שקורה הרבה בנושא סדרות.
קמת קושי בנוני.
רמזים:
פתרון
סעיף א
a7 * a3= 1
אנו מעוניינים למצוא את a5 לכן נציג את המשוואה בעזרת a5.
a5² = 1
a5 = 1 או a5 = -1
סעיף ב חלק ראשון
a5 = 1
אנו יודעים כי:
a1 * q4 = 1
a1 = 1 / q4
סעיף ב חלק שני
האם מתקיים:
בסדרה הנדסית מתקיים:
a9 = a5 * q4 = q4
a9 = q4
סעיף ב חלק שלישי
נביע את המשוואה שקיבלנו באמצעות a1, q שהם המשתנים שאנו עובדים איתם לאורך כל התרגיל ונקבל
נציב את הערך של a1 שאותו אנו יודעים במשוואה על מנת לצמצם משתנים:
a1 = 1 / q4
n – 5 = -8
n = -3
זה לא אפשרי, לכן אין איבר המקיים את זה.
סעיף ג חלק ראשון
אנו יודעים כי:
a1 = 1 / q4
מכך נוכל לדעת את כל 7 האיברים (משמאל לימין).
סעיף ג חלק שני
אנו רואים כי:
a4 * a6 = 1
a3 * a7 = 1
a2 * a8 = 1
a1 * a9 = 1
עבור a10 אין מספר שניתן להכפיל בו ולקבל 1.
כמו כן זו סדרה הנדסית אינסופית. החל מ a10 האיברים קטנים ואין להם מספר הופכי שמכפלתם יחד תיתן 1-.
לכן k = 9.
קיץ 2019 מועד ב
סעיף א
an+1 + an = 6n + 5
an + 1 = -an + 6n + 5
נבנה את המשוואה:
an+ 2 + an+1 = 6(n +1) + 5
ונציב בה את המשוואה הראשונה:
an+ 2 – an + 6n + 5 = 6(n +1) + 5
an+ 2 = an – 6n – 5 +6n + 6 +5
an+ 2 = an + 6
סעיף ב
אנו צריכים סדרה חשבונית שתקיים שני כללים:
an+1 + an = 6n + 5
an+ 2 = an + 6
נציב בכלל הנסיגה n =1 ונקבל:
a1 + a2 = 6 + 5 = 11
נציב כדוגמה a1 = 0 ונקבל את הסדרה
0,11,6,17
סעיף ג
כאשר הסדרה חשבונית אנו יכולים לבנות את המשוואה:
a3 = a1 + 2d
ובנוסף אנו יודעים:
an+ 2 = an + 6
a3 = a1 + 6
מכך נקבל:
d = 3
כמו כן אנו יודעים:
a1 + a2 = 11
a1 + a1 + 3 = 11
2a1 = 8
a1 = 4
סעיף ד
כאשר אנו מחשבים סכום של סדרה שהיא לא חשבונית ולא הנדסית עלינו לחשוב על האפשרות למצוא דרך מקורית לחשב את סכום הסדרה.
האיבר האמצעי הוא האיבר במקום ה n +1.
נסמן את ה an+ 1 של הסדרה החדשה בצבע אדום. את an+1 של הסדרה המקורית נשאיר שחור.
an+ 1 = an+1 – n – 1 = 43
an+1 – n – 1 = 43
נשים לב ש:
a1 = 4
d = 3
an+1 – n – 1 = 43
a1 + nd – n – 1 = 43
3n – n = 40
2n = 40
n =20
מספר האיברים בסדרה הוא:
2n +1 = 41.
חורף 2019
רמזים:
סעיף א
הרעיון של הפתרון
מכוון ששאלו אותנו על סכום נשתמש בנוסחת הסכום לחישוב הסכום.
מכוון שמופיע האיבר ה an+2 בנוסחה שקיבלנו נביע אותו בעזרת a1,d.
פתרון
נגדיר
d – הפרש הסדרה.
נחשב את ערך האיבר במקום ה an+2 על פי נוסחת האיבר הכללי.
an= a1 + (n – 1)d
an+2 = a1 + (n + 1)d
נחשב את סכום 2n + 3 איברי הסדרה.
נוסחת סכום סדרה חשבונית היא:
באגף ימין ניתן להוציא 2 מחוץ לסוגריים ולצמצם
נציב את המשוואה הזו
an+2 = a1 + (n + 1)d
(זה הביטוי הקיים בצד השמאלי של המונה).
ונקבל:
(S2n +3 = an +2 * (2n + 3
סעיף א2
נזהה את האיבר האמצעי של הסדרה.
בסדרה שבה 2n + 3 איברים (מספר אי זוגי) האיבר האמצעי הוא:
0.5(2n + 3 + 1) = n + 2
an + 2 הוא האיבר האמצעי.
על מנת למצוא את מספר האיברים נשתמש בנתון "סכום הסדרה גדול פי 43 מהאיבר האמצעי"
S2n +3 = 43 * an +2
בסעיף א מצאנו נוסחה אחרת לסכום:
(S2n +3 = an +2 * (2n + 3
נשווה את הנוסחאות:
an +2 * (2n + 3) = 43 * an +2
מכוון ש an +2 שונה מ 0 ניתן לצמצם אותו.
2n + 3 = 43 / -3
2n = 40 / : 2
n = 20
מספר האיברים הוא 2n + 3. לכן מספר האיברים הוא 43.
סעיף ב1
זיהוי האיבר האמצעי
עלינו למצוא את האיבר האמצעי.
בסדרה 43 איברים.
a22
הוא האיבר האמצעי אותו אנו מחפשים.
עבור סדרת המקומות האי זוגיים
a1 האיבר הראשון.
2d הפרש הסדרה
n+ 2 = 22 מספר האיברים.
לכן סכום המקומות האי זוגיים יהיה:
עבור סדרת המקומות הזוגיים:
a1 + d האיבר הראשון.
2d הפרש הסדרה
n+ 1 = 21 מספר האיברים.
לכן סכום המקומות הזוגיים הוא:
נתון כי סדרת המקומות האי זוגיים גדולה ב 40 לכן המשוואה היא:
נכפיל פי 2 ונקבל:
2a1 + 42d) * 22 = (2a1 + 42d) *21) + 80)
44a1+ 924d = 42a1 + 882d + 80
2a1 + 42d = 80
a1 + 21d = 40
האיבר האמצעי הוא האיבר במקום ה 22.
על פי נוסחת האיבר הכללי:
a22 = a1 + 21d
לכן האיבר האמצעי שווה ל 40.
סעיף ב2
סכום הסדרה גדול פי 43 מהאיבר האמצעי לכן הסכום הוא:
S = 43 * 40 = 1720
סעיף ג
סדרה עולה היא סדרה עם d חיובי, סדרה יורדת היא סדרה עם d שלילי.
לכן עלינו למצוא את d.
בסעיף הקודם מצאנו משוואה הכוללת את d.
a1 + 21d = 40
נציב d = -a1
ונקבל:
21d – d = 40
20d = 40 / : 20
d = 2
הפרש הסדרה חיובי ולכן הפונקציה עולה
סעיף ד
בכל איבר בסדרה החדשה יש k איברים.
עלינו לזהות באיזה איבר בסדרה המקורית ניתן להתחיל ועדיין לכלול k איברים.
בסדרה המקורית 43 איברים.
על מנת שהאיבר האחרון יוכל לכלול k איברים הוא צריך להתחיל במקום ה n + 1 – k
למשל אם k = 3.
אז האיבר האחרון יכלול את האיברים 41,42,43.
התשובה היא:
43 + 1 – k = 44 – k
קיץ 2018 מועד ב
סעיף א
ננסה למצוא את הקשר בין an+2 ל an.
מצאנו כי קיים יחס קבוע בין שני איברים המרוחקים שני מקומות אחד מהשני. לכן סדרת המקומות הזוגיים והאי זוגיים הן סדרות הנדסיות.
ההוכחה שעשינו תופסת לכל n, לא הגבלנו את ההוכחה ל n זוגי או אי זוגי.
סעיף ב חלק ראשון
נתון לנו
a3 = a1*c = -1
a5 = -1*c = -c
a7 = -c * c = -c²
נעבור לסדרת המקומות הזוגיים:
מכך ניתן למצוא את a2
a4 = a2*c = c
a6 = a4*c = c²
לסיכום שבעת האיברים הם:
a2 = 1
a3 = a1*c = -1
a4 = a2*c = c
a5 = -1*c = -c
a6 = a4*c = c²
a7 = -c * c = -c²
סעיף ב חלק שני
סכום שבעת האיברים הוא:
סעיף ב חלק שלישי
נחשב את סדרת המקומות הזוגיים ואת סדרת המקומות האי זוגיים ונחבר אותן.
בסדרת המקומות האי זוגיים n איברים.
בסדרת המקומות הזוגיים n-1 איברים.
הנוסחה לסכום סדרה הנדסית היא:
סכום המקומות האי זוגיים והזוגיים ביחד הוא:
(משמאל האי זוגיים, מימים הזוגיים)
נשים לב ש:
לכן נקבל:
ניצור במונה מכנה משותף של c.
לאחר מיכן נוציא מינוס מכנה משותף במכנה על על מנת שנוכל לצמצם.
מצאנו כי הסכום של 2n-1 איברים עוקבים הוא
ולכן הוא אינו תלוי ב n.
סעיף ג
נציב את הנוסחה של an+1 אל הנוסחה של bn ונקבל:
לכן bn+1 שווה ל:
נבדוק מה היא מנת החלוקה של איברים עוקבים.
מצאנו כי מנת איברים עוקבים היא מספר קבוע, ולכן זו סדרה הנדסית.
סעיף ג חלק שני
נתון כי c > 0.
הסדרה תהיה סדרה יורדת כאשר
וזה קורה כאשר c >1 (זו התשובה לסעיף).
סעיף ג חלק שלישי
על מנת לחשב את סכום הסדרה עלינו למצוא את b1.
נוסחת האיבר הכללי היא:
ולכן האיבר הראשון הוא:
נציב בנוסחת סכום סדרה הנדסית אינסופית ונקבל את התשובה:
קיץ 2018 מועד א
השאלה היא על סדרה הנדסית אינסופית.
בפתרון נעבוד עם נוסחאות ונציב נוסחה בנוסחה על מנת לפתור.
סעיפים א,ד יכולים להראות "כמתחכמים".
רמזים
פתרון
סעיף א
סכום סדרה הנדסית מתכנסת ניתן על ידי הנוסחה:
ובסדרה הנדסית מתכנסת
-1 < q < 1
לכן בסדרה הנדסית מתכנסת המכנה תמיד חיובי.
לכן הדבר היחידי שגורם לסכום להיות שלילי הוא a1 < 0.
התשובה היא ג.
סעיף ב
T + pR = 0
נביע את T,R באמצעות נוסחת הסכום q,a1 וכך נוכל להגיע אל התשובה.
עבור סדרת המקומות האי זוגיים
a1' = a1
q' = q²
לכן סכום איברי המקומות האי זוגיים הוא:
עבור סדרת המקומות הזוגיים:
a1" = a1q
q" = q²
לכן סכום המקומות הזוגיים הוא:
נציב את הערכים של T,R בנוסחה:
T + pR = 0
p*q + 1 = 0 /-1
p*q = -1 / : q
p = -1/q
סעיף ג
הסדרה b היא סדרה מתכנסת אם:
-1 < p < 1
אנו יודעים כי q הוא מספר בתחום הזה.
1- חלקי שבר קטן ממינוס אחד או גדול מ 1.
p = -1/q
לכן סדרה הנדסית ש p הוא המנה שלה אינה סדרה מתכנסת.
סעיף ד
בסעיף ב מצאנו:
p*q = -1
q = -1 / p
אם p שלילי אז q חיובי.
כמו כן מצאנו בסעיף א ש a1 < 0
מכאן נפתור בשתי דרכים: הסבר מילולי והוכחה מתמטית
הסבר מילולי
0 < q < 1
כאשר נכפיל את a1 שהוא מספר שלילי ב q המכפלה תגדל, וכך יהיה כל פעם שנכפיל ב q.
לכן הסדרה an היא סדרה עולה.
דרך שנייה: הוכחה מתמטית
נבצע את פעולת החיסור
an+1 – an
ואם התוצאה חיובית אז
an+1 > an
(an+1 – an = a1qn – a1qn-1 = a1qn-1(q -1
הביטוי a1qn-1 הוא שלילי כי a1 שלילי ו q חיובי.
הביטוי q -1 שלילי כי q < 1.
מכפלת שני ביטויים שליליים היא חיובית ולכן הוכחנו ש:
an+1 – an > 0
ולכן זו סדרה עולה.
*הערה: השתמשנו בסעיף זה בהוכחה מתמטית מסורבלת לדבר פשוט.
יתכן שבודק הבחינה היה מקבל גם את ההוכחה המילולית הבאה.
a1 < 0
q הוא מספר חיובי הקטן מ 1 ולכן תוצאת המכפלה:
a1qn גדלה ככול ש n גדול יותר.
קיץ 2017 מועד א
על מנת לדעת פרטים על הסדרה bn עלינו לדעת ערכים של שני איברים שלה.
b6 = 64
נמצא את b3 על ידי מציאת a3.
נמצא את a3.
b3 = a3+c3 = 7.875 + 0.125 = 8
נמצא את q:
q=2
נמצא את האיבר הראשון
b3 = b1q²
8 = 4b1
b1 = 2
תשובה: b1 = 2. q=2.
חלק שני.
c1 = b1-a1
נמצא את a1.
c1 = 2-1.5=0.5
c3 / c1 = q² = 0.125 / 0.5 = 0.25
q² = 0.25
q=0.5
תשובה: q=0.5, c1 = 0.5.
סעיף ב
an = bn – cn נתון.
cn = bn– an
קיבלנו כי כל איבר בסדרה cn שווה להפרש האיברים המתאימים בסדרות bn, an לכן סכום ההפרשים בסדרות bn, an שווה לסכום הסדרה cn.
c1 = b1 – a1
……..
cn = bn – an
כאשר נחבר את הטורים נקבל:
Cn = Bn – An
סעיף ג:
0.9 < Bn – An < 1
על פי מה שמצאנו הסעיף הקודם:
0.9 < Cn < 1
נתון כי c היא סדרה הנדסית.
נציב את הערכים q=0.5, c1 = 0.5 בנוסחה לסכום סדרה הנדסית ונקבל ביטוי המייצג את סכום סדרה C.
0.9 < Cn < 1
0.9 < -(0.5n – 1) < 1
נפתור עכשיו את שני האי שוויונות:
0.5n-1)<1)-
1-0.5n <1
0.5n<0-
אי שוויון זה מתקיים לכל n חיובי ושלם.
0.5n-1)>0.9)-
1-0.5n >0.9
0.5n<0.1
0.5n זה ביטוי שהולך וקטן ככל ש n עולה.
לכן עלינו למצוא עבור איזה ערך n האי שוויון יתקיים בפעם הראשונה.
וזה גם יתקיים עבור כל n גדול ממנו.
נבדוק טכנית מתי זה קורה:
0.5³ = 0.125 >0.1
0.54 = 1/16 <0.1
n = 4
הוא האיבר הראשון שמקיים את האי שוויון.
האי שוויון מתקיים גם עבור n > 4.
לכן התשובה היא n ≥ 4.
חורף 2017
(an+1 = an / (4an+3
bn = (1/an) +2 = (2an+1) / an
bn =2+(4an+3) / an
bn+1 = 2+(4an+1+3) / an+1 = (6an+1+3) / an+1
נציב את (an+1 = an / (4an+3 במשוואה.
bn+1 = 6an / (4an+3) +3 / an / (4an+3) = 6an+3 / an
bn+1 / bn = (6an+3 / an) / (2an+1) / an) = (6an+3) / (2an+1) = 3
מצאנו כי לסדרה bn מנה קבועה (3) שאינה תלויה ב n ולכן זו סדרה הנדסית.
סעיף ב
נמצא את b1.
b1 = 1/-1 +2=1
הנוסחה של bn על פי הנוסחה לאיבר הכללי של סדרה הנדסית:
bn = 1*3n-1 = 3n-1
ננסה למצוא את הקשר בין הסדרה d = 1/a1 + ….+ 1/an לבין bn.
אנו יודעים כי bn = (1/an) +2
bn -2 = 1/an
כלומר:
b1 -2 = 1/a1
b2 -2 = 1/a2
b3 -2 = 1/a3
אנו רואים כי סכום הסדרה d = 1/a1 + ….+ 1/an הוא סכום הסדרה bn פחות 2n.
נגדיר את סכום הסדרה ההנדסית bn.
Sn = (3n -1) / 2
לכן סכום הסדרה d = 1/a1 + ….+ 1/an הוא:
Sbn = 0.5(3n -1)-2n – תשובה סופית.
סעיף ג
עלינו לחשב את סכום הסדרה:
k = 1/a1 -1/a2+1/a3 – 1/a4….+1/an-1 -1 1/an
אם נציב bn -2 = 1/an במקום איברי הסדרה נקבל:
(k =(b1-2)- (b2-2) +(b3-2) – (b4-2)…+(bn-1-2)- (bn-2
ניתן לראות שכאשר פותחים סוגריים אנו נשארים עם הביטוי:
k = b1 – b2+b3– b4 + … +bn-1 – bn
שימו שכל מספרי ה 2 מתבטלים בגלל שידוע שמספר איברי הסדרה הוא זוגי. אם המספר היה אי זוגי היינו נשארים עם 2 אחד.
הסדרה שמצאנו היא סדרה הנדסית שבה q=-3 ו a1=1. הסכום של סדרה זו הוא:
S =((-3)n-1) / -4
מכוון ש n זוגי ניתן לרשום גם:
S =((3)n-1) / -4
קיץ 2016 מועד א
a4+ a8 + a12 + a16 = 224
נשתמש בנוסחה לאיבר הכללי על מנת להגדיר משוואה זו רק באמצעות a1, d.
a4 = a1+ 3d
a8 = a1+ 7d
a12 = a1+ 11d
a16 = a1+ 15d
נציב:
a4 + a8 + a12 + a16 = 4a1 + 36d= 224
a1 + 9d)4 = 224)
a1 + 9d = 56 – זו משוואה 1.
נשתמש בנוסחה לסכום סדרה חשבונית על מנת לחשב את סכום 19 האיברים.
(s19 = 9.5 (2a1+ 18d
s19 = 19(a1+ 9d)
נציב את משוואה 1 בביטוי זה:
s19 = 19*56 = 1064
תשובה: s19 = 1064.
סעיף ב.
sn = n*an
נגדיר את שני צדדי המשוואה בעזרת a1, d.
נצמצם את n ונקבל:
a1 + 0.5dn – 0.5d = a1 + dn – d
0.5d(n – 1)=0
n-1= 0 לא יתכן כי בסדרה קיים a16
0.5d = 0
d=0
סעיף ג.
אנו יודעים כי:
a1 + 9d = 56
a1 + 0 = 56
a1 = 56
סעיף ד.
bn+1 – bn = an + sn
צריך למצוא את הסכום של:
(b2– b1) – (b3-b2) + (b4-b3) … + (b20 – b19)
על מנת לחשב את הסכום עלינו להוכיח כי bn היא סדרה חשבונית.
אנו יודעים כי: sn = n*an
bn+1 – bn = an + sn
(bn+1 – bn = an + n * an = an * (1+n
נחסר בין שני איברים סמוכים בסדרה bn על מנת להראות שההפרש הוא מספר קבוע.
(bn+1 – bn – (bn-bn-1 =
אנו יודעים כי:
(bn+1 – bn = an (1+n
bn-bn-1 = an-1 * n
(an (1+n) – (an-1 * n
בסדרה an הפרש הסדרה הוא 0 ולכן an = an-1 = 56
an (1+n) – (an-1 * n = 56 + 56n – 56n = 56
מצאנו כי הפרש הסדרה הוא מספר קבוע ולכן זו סדרה חשבונית שהפרשה הוא 56.
נמצא את האיבר הראשון בסדרה (n=1):
b2 – b1 = an (1 + n) = 56*2 =112
נציב a1 = 112, d = 56, n = 19 בנוסחה לסכום סדרה חשבונית.
דרך נוספת לחישוב סכום הסדרה
נשתמש בכך שאנו יודעים שיש בסדרה 19 איברים:
(b2– b1) – (b3-b2) + (b4-b3) … + (b20 – b19)
ולכן ניתן לחשב כל אחד מיהם ספציפית:
t1 = b2-b1 = an (1+n)=56*2=112
t2 = b3-b2 = a2 (1+2)=56*3=168
וכך הלאה, כל איבר גדול מקודמו ב 56.
לכן 19 האיברים הם:
112+168+224+280…. = 11,704























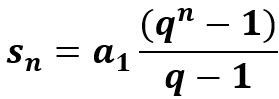






יש לך טיפים או מילון מושגים שיכול לעזור להבנת מה שדורשים מאיתנו בסדרות
לדוגמא: יחס=לחילוק
תודה רבה האתר הכי שווה שיצא לי ללמוד ממנו !
שלום
הנושא של סדרות באתר עדיין לא כולל את הדברים הללו.
כל הכבוד אתר מעולה!!
בכיף